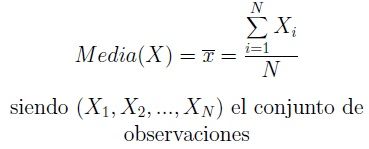Desviación tipica

"La desviación típica es la raíz cuadrada de la varianza.

Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.

 La desviación típica se representa por σ.

Desviacion Típica para datos agrupa     

                         

Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.

https://www.vitutor.com/estadistica/descriptiva/a_16.html

Ejemplo: 

• Calcular la desviación estándar de las siguientes puntuaciones de un jugador de baloncesto en los últimos partidos:
• Puntuaciones: 18, 20, 20, 22, 20, 20
• Calculamos la media aritmética ():  
• Número de valores: 6
• Media Aritmética = (18 + 20 + 20 + 22 + 20 + 20) / 6 = 120 / 6 = 20
• Calculamos la Desviación Estándar:
• σ² = [(18-20)² + (20-20)² + (20-20)² + (22-20)² + (20-20)² + (20-20)²] / 6 = 16 / 6 = 8 /3 = 2,67
• Desviación estándar: σ = √ 2,67 = 1,63" http://www.matematicas10.net/2017/02/ejemplos-de-desviacion-estandar.html 

Moda

"La moda es el valor que tiene mayor frecuencia absoluta. Se representa por M_o. Se puede hallar la moda para variables cualitativas y cuantitativas.

Hallar la moda de la distribución:

2, 3, 3, 4, 4, 4, 5, 5 M_o = 4

Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.

1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9M_o= 1, 5, 9

Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.

2, 2, 3, 3, 6, 6, 9, 9

Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.

0, 1, 3, 3, 5,

el calculo de la moda para datos agrupados se hacen los siguientes pasos con la siguiente formula:  

Todos los intervalos tienen la misma amplitud.

L_i es el límite inferior de la clase modal.

f_i es la frecuencia absoluta de la clase modal.

f_i--1 es la frecuencia absoluta inmediatamente inferior a la clase modal.

f_i-+1 es la frecuencia absoluta inmediatamente posterior a la clase modal.

a_i es la amplitud de la clase.

También se utiliza otra fórmula de la moda que da un valor aproximado de ésta:

2º Los intervalos tienen amplitudes distintas.

En primer lugar tenemos que hallar las alturas.

La clase modal es la que tiene mayor altura.

La fórmula de la moda aproximada cuando existen distintas amplitudes es:

ejemplos cuando todos los intervalos tienen las mismas amplitud 

calcular la moda de una distribución estadística que viene dada por la siguiente tabla:

	fi
[60, 63)	5
[63, 66)	18
[66, 69)	42
[69, 72)	27
[72, 75)	8
	100

 

  " https://www.vitutor.com/estadistica/descriptiva/a_8.html

Mediana

"La mediana de un conjunto de datos es el valor que cumple que la mitad de valores están por encima y la otra mitad por debajo. Así pues, para encontrarla basta con ordenar los elementos de menor a mayor y escoger el valor central.

Caso 1: El número de valores es impar.

Se tienen los siguientes 5 valores: .10, 5, 12, 3, 14

Se ordenan 3, 5,12, 14, 19 y se toma el valor central: 12 cumple que hay dos valores por encima y dos por debajo.

Caso 2: El número de valores es par.
Los 6 valores son 4, 6, 5, 7, 3, 9 Se ordenan 3, 4, 5, 6, 7, 9 y se toman los dos valores centrales, 5 y 6
La mediana será el promedio de ambos: 5+6/2= 5,5

Ejemplo: Encontrar la mediana de la siguiente lista de números de una ruleta rusa:
0, 13, 14, 16, 19, 20, 21, 22, 30,36
Se realiza el promedio de los dos números centrales 19 y 20
a mediana es 19,5" https://www.sangakoo.com/es/temas/la-mediana

Media Aritmética

La media X (también llamada promedio o media aritmética) de un conjunto de datos (X₁,X₂,…,X_N) es una medida de posición central. La definimos como el valor característico de la serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.

Es decir:

La desventaja de la media aritmética es que si hay valores extremos alejados  no resulta el promedio más indicado. 

A continuación un ejemplo de la Media Aritmética  

   

Tenemos las edades de los once jugadores de un equipo de fútbol y queremos calcular su media. 29, 31, 20, 19, 26, 25, 26, 30, 18, 23 y 26 

                                                                                           

Para ello, sumamos todas las edades y las dividimos por el número total de elementos, o sea once jugadores.

Tipos de Cuadros Estadísticos

"la mayor ventaja de trabajar expresando información en diferentes tipos de gráficas estadísticas, es que todas ellas nos darán información clara y rápida del conjunto de datos  obtenidos en el estudio o investigación en cuestión.

Un detalle importante a señalar es que existen varios tipos de gráficas estadísticas y que cada una de será adecuada para diferentes tipos de  estudios. En otras palabras, hay estudios donde se busca comparar, otros buscan detectar mayorías o minorías, otros quieren determinar tendencias, otros incidencias, etc.

En todos los casos, uno en especial será el gráfico más adecuado y claro. Los gráficos estadísticos más usuales son:

• Gráfico o diagrama de barras
• Gráfico o diagrama de sectores
• Histograma
• Polígono de frecuencias"  https://matematicasmodernas.com/tipos-de-graficas-estadisticas/

A  continuación veremos detalladamente como se construyen estos cuadros en Microsoft Officce Exel

PASOS: 1-  se tiene que construir una tabla de datos de lo que se quiere registrar.

2- luego en la barra de herramientas selecciona la opción de INSERTAR 

3- seleccionan la opción de COLUMNA y allí se encontrara muchos tipos de gráficos que serán depende de su uso el que se utilizara   

Y ya podemos empezar a trabajar con Exel y utilizar los diferentes tipos de gráficos. 

A continuación mostraremos los diferentes tipos de gráficos:

•  Diagrama de barras 

•    Diagrama de sectores

• Histograma

    

• Polígono de frecuencias

Variables en Estadísticas

"Una variable estadística es una característica que puede fluctuar y cuya variación es susceptible de adoptar diferentes valores, los cuales pueden medirse u observarse. Las variables adquieren valor cuando se relacionan con otras variables, es decir, si forman parte de una hipótesis o de una teoría. En este caso se las denomina constructor o construcciones hipotéticas." https://es.wikipedia.org/wiki/Variable_estad%C3%ADstica  

Existen diferentes tipos de variables que veremos a continuación:

• " Variable cualitativa: Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos: 

1. Variable cualitativa nominal:  Una variable cualitativa nominal presenta modalidades no numéricas que no admiten un criterio de orden. ejemplo: El estado civil, con las siguientes modalidades: soltero, casado, separado, divorciado y viudo.
2. Variable cualitativa ordinal o variable cuasicuantitativa: Una variable cualitativa ordinal presenta modalidades no numéricas, en las que existe un orden. ejemplo: La nota en un examen: suspenso, aprobado, notable, sobresaliente o también Medallas de una prueba deportiva: oro, plata, bronce.

• Variable cuantitativa: Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:

1. Variable discreta:  Una variable discreta es aquella que solo puede tomar un número finito de valores entre dos valores cualesquiera de una característica. ejemplo:  El número de hermanos de 5 amigos: 2, 1, 0, 1, 3. 
2. Variable continua:Una variable continua es aquella que puede tomar un número infinito de valores entre dos valores cualesquiera de una característica. ejemplo: La altura de los 5 amigos: 1.73, 1.82, 1.77, 1.69, 1.75." https://www.vitutor.com/estadistica/descriptiva/a_2.html

• " Variables independientes: 

  Una variable independiente es aquella cuyo valor no depende de otra variable. Es aquella característica o propiedad que se supone es la causa del fenómeno estudiado. En investigación experimental se llama así a la variable que el investigador manipula.
  Las variables independientes son las que el investigador escoge para establecer agrupaciones en el estudio, clasificando intrínsecamente a los casos del mismo. Un tipo especial son las variables de control, que modifican al resto de las variables independientes y que de no tenerse en cuenta adecuadamente pueden alterar los resultados por medio de un sesgo. ejemplo: El número de palomas que hay en una ciudad es independiente del número de profesores de inglés que hay en esa misma ciudad. Son conceptos no relacionados.
• Variables dependientes: Una variable dependiente es aquella cuyos valores dependen de los que tomen otra variable. La variable dependiente en una función que suele representar por y. La variable dependiente se representa en el eje ordenadas. Son las variables de respuesta que se observan en el estudio, y que podrían estar influidas por los valores de las variables independientes. ejemplo:  dependiente: Ganancia de una empresa independiente: cantidad de productos vendidos." https://es.wikipedia.org/wiki/Variable_estad%C3%ADstica 

Estadísticas

Tenemos que tener claro que la palabra Estadística no es igual a Estadísticas.
"Estadísticas también se refiere al resultado de aplicar los logaritmos estadísticos a un conjunto de datos, como en estadísticas económicas, estadísticas criminales , etcétera." https://es.wikipedia.org/wiki/Estad%C3%ADstica 

Estadística

"La estadística ​es una rama de las matemáticas y una herramienta que estudia usos y análisis provenientes de una muestra representativa de datos, que busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional." https://es.wikipedia.org/wiki/Estad%C3%ADstica 

También podría decirse que, "La estadística es la ciencia de los datos, la cual implica su recolección, clasificación, síntesis, organización, análisis e interpretación, para la toma de decisiones frente a la incertidumbre (Ángel, p. 28)" https://www.gestiopolis.com/que-es-estadistica-tipos-y-objetivos/